Helper for Bézier Curves, Triangles, and Higher Order Objects
Project description
Helper for Bézier Curves, Triangles, and Higher Order Objects
This library provides:
Dive in and take a look!
Why Bézier?
A Bézier curve (and surface, etc.) is a parametric curve that uses the Bernstein basis:
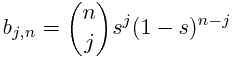
to define a curve as a linear combination:
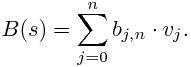
This comes from the fact that the weights sum to one:
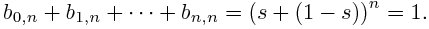
This can be generalized to higher order by considering three, four, etc. non-negative weights that sum to one (in the above we have the two non-negative weights s and 1 - s).
Due to their simple form, Bézier curves:
can easily model geometric objects as parametric curves, surfaces, etc.
can be computed in an efficient and numerically stable way via de Casteljau’s algorithm
can utilize convex optimization techniques for many algorithms (such as curve-curve intersection), since curves (and surfaces, etc.) are convex combinations of the basis
Many applications – as well as the history of their development – are described in “The Bernstein polynomial basis: A centennial retrospective”, for example;
Installing
bezier can be installed with pip:
$ python -m pip install --upgrade bezier
$ python2.7 -m pip install --upgrade bezier
$ python3.6 -m pip install --upgrade bezierbezier is open-source, so you can alternatively grab the source code from GitHub and install from source.
Getting Started
For example, to create a curve:
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)The intersection (points) between two curves can also be determined:
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.5, 0.75, 1.0],
... [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> curve2 = bezier.Curve.from_nodes(nodes2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.31101776, 0.68898224, 0. , 1. ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> points
array([[0.31101776, 0.68898224, 0. , 1. ],
[0.42857143, 0.42857143, 0. , 0. ]])and then we can plot these curves (along with their intersections):
>>> import matplotlib.pyplot as plt
>>> import seaborn
>>> seaborn.set()
>>>
>>> ax = curve1.plot(num_pts=256)
>>> _ = curve2.plot(num_pts=256, ax=ax)
>>> lines = ax.plot(
... points[0, :], points[1, :],
... marker='o', linestyle='None', color='black')
>>> _ = ax.axis('scaled')
>>> _ = ax.set_xlim(-0.125, 1.125)
>>> _ = ax.set_ylim(-0.0625, 0.625)
>>> plt.show()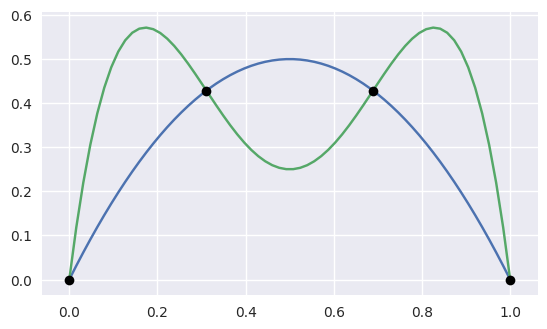
For API-level documentation, check out the Bézier Package documentation.
Development
To work on adding a feature or to run the functional tests, see the DEVELOPMENT doc for more information on how to get started.
License
bezier is made available under the Apache 2.0 License. For more details, see the LICENSE.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distributions
Hashes for bezier-0.8.0-cp36-none-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | c7bc1ccbd21be9106e16920ea8a5680a41eed35756ec0f7ce133a0e914cbb1f6 |
|
| MD5 | 35ca697a35a1b970f0d5e678e222003f |
|
| BLAKE2b-256 | 547c90c39bb4c5aed24c2b0bc6758af017d29f146e75c9aa2c24971c113acf4c |
Hashes for bezier-0.8.0-cp36-none-win32.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 333445e995e59f880e8b98ce1006f15d6173578738b2aaabc56ba8adab80092f |
|
| MD5 | 4dab35e041cac46223b3c6cce8c2eb95 |
|
| BLAKE2b-256 | c1b5a29cfa0d145c5a44eab77787df16d9568aaf44c85cfdf7c485c451ba9838 |
Hashes for bezier-0.8.0-cp36-cp36m-manylinux1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 8aba901679e309653072399a61cc32640de3883fc0fc6768bf28938e44698f50 |
|
| MD5 | 1f347f6fd0794eef46853e4c6336bc7c |
|
| BLAKE2b-256 | 2908131e81c80db7e78e0ccd8a68c79489d91de080429f3301d418d05918bad1 |
Hashes for bezier-0.8.0-cp36-cp36m-manylinux1_i686.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 7f6498aeb739e5eb4a595106ed5fcb5f9bf0392a8ea710c51b1b9dd61ca36b99 |
|
| MD5 | c7c04713482bd3491e6bc3782bb1f212 |
|
| BLAKE2b-256 | d68e8aa7b9eec1522793234999be7a45dd8e83ee98cb0e53eee457a6c435f3a2 |
Hashes for bezier-0.8.0-cp36-cp36m-macosx_10_6_intel.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 6a2c7dbecc740ea54f1cdb7917f302b578ca2e8d6dcc49fb388d12454e4f5e7a |
|
| MD5 | 99fd27fdc41de18dc35b48acd7f14193 |
|
| BLAKE2b-256 | ede5fc978b621ba1d7ab39728257de11ace250feb2cfdeee4050cbdf265ae6b2 |
Hashes for bezier-0.8.0-cp35-none-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 8b8be73b97271623b5e2e52555d11468d4804d3ad09d0f5e3a93db1c31b43b46 |
|
| MD5 | a2954f0825eee7568f551e876769032b |
|
| BLAKE2b-256 | 8d3ad36e81b09f4604d8ac190b159b5dd9645a7c636e8e6711b7074537d6bc04 |
Hashes for bezier-0.8.0-cp35-none-win32.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | f1fcaaeebec3b3cbb1ffc9f40f697e62a30320d4c296d271df014742f8217a51 |
|
| MD5 | 91475ebffff7b195ac0de36e05cc0d31 |
|
| BLAKE2b-256 | 45115cf09fa9f4dbb116a7c4f3e36f9fe0f8bb65662126b1a02b7d91365e6c65 |
Hashes for bezier-0.8.0-cp35-cp35m-manylinux1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 287d1054accf6679f3f3ebb7d631627dc9d5f7d2a69fa823e189c6c5857fa92f |
|
| MD5 | 3aaa7b465c5d634b3d54f584e1293b8d |
|
| BLAKE2b-256 | 817e9ab72386ea08b0ee9ab8bbf8e3e91ccd5741be2eea5fb3d7cf9240ae86f4 |
Hashes for bezier-0.8.0-cp35-cp35m-manylinux1_i686.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | f266ba98579463ad88dd451ab8219f64d89b9993ebc1f177e8bbf5882cdd768f |
|
| MD5 | 0f4bfb89d566add14ae168494a852e45 |
|
| BLAKE2b-256 | 5a47db72f06ca4434efc719256654931626fb60d40f8ca1078f4f059ddc1b959 |
Hashes for bezier-0.8.0-cp35-cp35m-macosx_10_6_intel.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | e9470d4dd3c85ed862d1a968328ae83ed70434f0366c147c16e625647796e03e |
|
| MD5 | c9e5b9cac4ef2dee42e25226c515b3b7 |
|
| BLAKE2b-256 | eee9dccae4bb58e8c3e4fd2b48d8e3b9205ae48184493f191cfdff22ee6fcdb2 |
Hashes for bezier-0.8.0-cp27-none-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | aa8ac4bb393dc8fcb06956e555fe7bda14fcd769be6497006335415b5159acde |
|
| MD5 | b361cf3af40fe3562b20a7f162b22cab |
|
| BLAKE2b-256 | e9d8b5bebd0371d105a8e811298dfa06993e3552e15fb1f71743f9f63994802e |
Hashes for bezier-0.8.0-cp27-none-win32.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 31c0ff2a27351f9aaa8806c1bd70898377fb737d31eed8e2176e0893258123dc |
|
| MD5 | 8235bc2fd6cdbbfc703754491f1c82d3 |
|
| BLAKE2b-256 | a5a398b058abc12591e018f89a9433ded8a32fdcc91c403dc90e2e0cb01f3089 |
Hashes for bezier-0.8.0-cp27-cp27mu-manylinux1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 3c670e0388245e47957e796c32f65dfa05c20685af51e68f78ce61983ee568b3 |
|
| MD5 | f471c03eaa2b037c2e7717e2edc61f56 |
|
| BLAKE2b-256 | 1d93a3937e9953f40084b73137089d6e8d746548740e74e86d15b32f440464dc |
Hashes for bezier-0.8.0-cp27-cp27mu-manylinux1_i686.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | f138c6fb8da653abd64ce479c2e0a036640242bbbb80eee1813cfcbc3f85789b |
|
| MD5 | 258cceba785496965020869594062daa |
|
| BLAKE2b-256 | 2f97023c076088a261c5d36158b65ebf35f9b813a262f1aa14e570cc0ce8a448 |
Hashes for bezier-0.8.0-cp27-cp27m-manylinux1_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 3b0dc4196e88a0135f7b239c68cdb9c7a502c6776eb53993f029be8ba5d9b64d |
|
| MD5 | 7d1491eb0c4c8c9eb6d399b2a4354a28 |
|
| BLAKE2b-256 | 3128c73b1ef5032374284cf9483f76f03d0e0e84523cfd91819be015df051943 |
Hashes for bezier-0.8.0-cp27-cp27m-manylinux1_i686.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 16dc85ba34a63f95063b473e85dcd496dde1bf3f6e09d0b11ee6d483297a8a93 |
|
| MD5 | da495014507f4feb8618b7ebba253147 |
|
| BLAKE2b-256 | 8916cb3ae2734201fc450cd7151267f2a2ccd2a70c9df6d77d0c3be041594133 |
Hashes for bezier-0.8.0-cp27-cp27m-macosx_10_6_intel.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 8bd8cfe9185c6abd3af16fb7c77fcb61ba60390a7f72790a79c99f2ecaac0023 |
|
| MD5 | 1f49d17ded7b736b6ec86e90aeb28ac5 |
|
| BLAKE2b-256 | 076f97e02ad168cf0900d1c61372f466a10b0a4117a312263121a741cd39dcc9 |


















