Cubic spline interpolation on multidimensional grids in PyTorch
Project description
torch-cubic-spline-grids
Cubic spline interpolation on multidimensional grids in PyTorch.
The primary goal of this package is to provide learnable, continuous parametrisations of 1-4D spaces.
Overview
torch_cubic_spline_grids provides a set of PyTorch components called grids.
Grids are defined by
- their dimensionality (1d, 2d, 3d, 4d...)
- the number of points covering each dimension (
resolution) - the number of values stored on each grid point (
n_channels) - how we interpolate between values on grid points
All grids in this package consist of uniformly spaced points covering the full extend of each dimension.
First steps
Let's make a simple 2D grid with one value on each grid point.
import torch
from torch_cubic_spline_grids import CubicBSplineGrid2d
grid = CubicBSplineGrid2d(resolution=(5, 3), n_channels=1)
grid.ndimis2grid.resolutionis(5, 3)(or(h, w))grid.n_channelsis1grid.data.shapeis(1, 5, 3)(or(c, h, w))
In words, the grid extends over two dimensions (h, w) with 5 points
in h and 3 points in w.
There is one value stored at each point on the 2D grid.
The grid data is stored in a tensor of shape (c, *grid_resolution).
We can obtain the value (interpolant) at any continuous point on the grid.
The grid coordinate system extends from [0, 1] along each grid dimension.
The interpolant is obtained by sequential application of
cubic spline interpolation along each dimension of the grid.
coords = torch.rand(size=(10, 2)) # values in [0, 1]
interpolants = grid(coords)
interpolants.shapeis(10, 1)
Optimisation
Values at each grid point can be optimised by minimising a loss function associated with grid interpolants. In this way the continuous space of the grid can be made to more accurately model a 1-4D space.
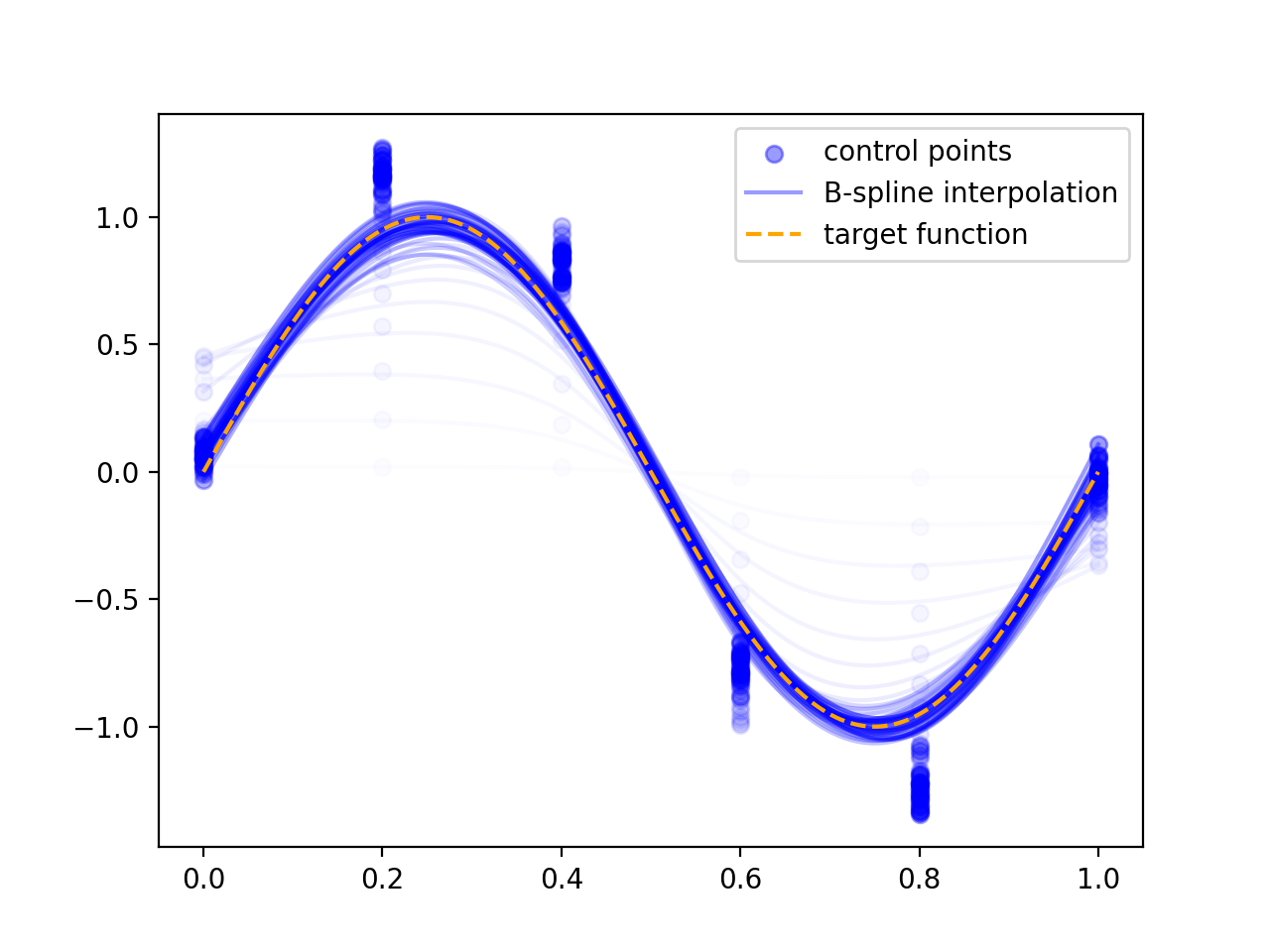
The image above shows the values of 6 control points on a 1D grid being optimised such that interpolating between them with cubic B-spline interpolation approximates a single oscillation of a sine wave.
Notebooks are available for this 1D example and a similar 2D example.
Types of grids
torch_cubic_spline_grids provides grids which can be interpolated with cubic
B-spline interpolation or cubic Catmull-Rom spline interpolation.
| spline | continuity | interpolating? |
|---|---|---|
| cubic B-spline | C2 | No |
| Catmull-Rom spline | C1 | Yes |
If your need the resulting curve to intersect the data on the grid you should use the cubic Catmull-Rom spline grids
CubicCatmullRomGrid1dCubicCatmullRomGrid2dCubicCatmullRomGrid3dCubicCatmullRomGrid4d
If you require continuous second derivatives then the cubic B-spline grids are more suitable.
CubicBSplineGrid1dCubicBSplineGrid2dCubicBSplineGrid3dCubicBSplineGrid4d
Regularisation
The number of points in each dimension should be chosen such that interpolating on the grid can approximate the underlying phenomenon being modelled without overfitting. A low resolution grid provides a regularising effect by smoothing the model.
Installation
torch_cubic_spline_grids is available on PyPI
pip install torch-cubic-spline-grids
Related work
This is a PyTorch implementation of the way Warp models continuous deformation fields and locally variable optical parameters in cryo-EM images. The approach is described in Dimitry Tegunov's paper:
Many methods in Warp are based on a continuous parametrization of 1- to 3-dimensional spaces. This parameterization is achieved by spline interpolation between points on a coarse, uniform grid, which is computationally efficient. A grid extends over the entirety of each dimension that needs to be modeled. The grid resolution is defined by the number of control points in each dimension and is scaled according to physical constraints (for example, the number of frames or pixels) and available signal. The latter provides regularization to prevent overfitting of sparse data with too many parameters. When a parameter described by the grid is retrieved for a point in space (and time), for example for a particle (frame), B-spline interpolation is performed at that point on the grid. To fit a grid’s parameters, in general, a cost function associated with the interpolants at specific positions on the grid is optimized.
For a fantastic introduction to splines I recommend Freya Holmer's YouTube video.
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file torch_cubic_spline_grids-0.0.8.tar.gz.
File metadata
- Download URL: torch_cubic_spline_grids-0.0.8.tar.gz
- Upload date:
- Size: 148.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | fd16315635eb7d0e2a97c8982c6f878c20edf875532b3a0f980280065b4a5353 |
|
| MD5 | 12373a0a752d89452e21fe7aecd53be1 |
|
| BLAKE2b-256 | b9e724dd5f302a0f80c7fd66d3744f5e3e90d06fe2dd98450efcb6cbb9a25a54 |
File details
Details for the file torch_cubic_spline_grids-0.0.8-py3-none-any.whl.
File metadata
- Download URL: torch_cubic_spline_grids-0.0.8-py3-none-any.whl
- Upload date:
- Size: 14.4 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 6d0de7aac91136120dc33e20f7e620fe4c3763b6b74f585e363f026cb1a58dc1 |
|
| MD5 | c68209f8908c18d9192e10fe18ceab30 |
|
| BLAKE2b-256 | ed33dbcd43ae6b682778690ca285733d561f47ba78a2534e34c98372ca2f8a7f |
















